In this post, I will illustrate Markov Property, Markov Reward Process and finally Markov Decision Process, which are fundamental concepts in Reinforcement Learning.

 

Markov Property

'The state is independent of the past given the present'

 

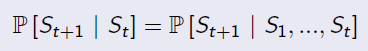
Markov Process (Markov Chain)

Keywords: state, transition matrix

A Markov Process is defined by a Tuple(S,P), in which S is the state space, and P is the transition matrix. The following chart is an example.

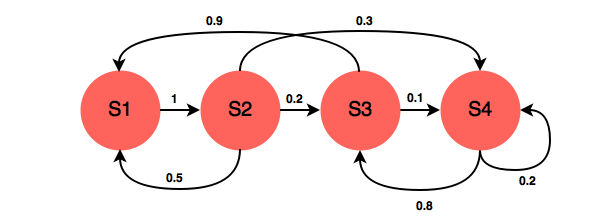
A transition matrix demonstrates the probabilities of transitioning from one state to another.

In the example above, the transition matrix is:

 

Markov Reward Process: Markov Process with Value Judgement

Keywords: Reward, Return, Discount Factor, Value Function

MRP add two additional properties into Markov Chain: one is Reward, who represents the immediate feedback an agent can receive at time t+1 if he is in state s at time t; another property is Discount Factor γ∈[0,1]. So the representation tuple is [S,P,R,γ].

 

Formally, Reward is the immediate feedback, which means when agent gets to state s at time t, it can definetly receive this reward at time t+1. It is defined by:

 

Given reward and discount factor, we can calculate the Return for a given senario by this equation:

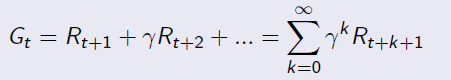
Example for Return calculation:

Senario: Class1->Class2->Class3->Pass->Sleep, and the agent is at state=Class1.

Case 1: when gamma=0, g=-2+(-2)*0+(-2)*0+10*0=-2

Case 2: when gamma=1, g=-2+(-2)*1+(-2)*1+10*1=4

Case 3: when gamma=0.8, g=-2+(-2)*0.8+(-2)*0.64+10*=-4-1.6+5.12=-0.48

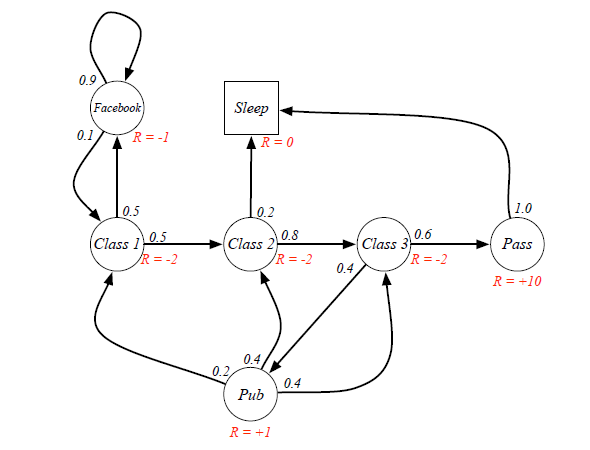
From different γ, we know our agent can be exetremely short-sighted (far-sighted) only for immediate reward, or trying to seek balance between short and long term reward.

 

When an agent is in a certain state, the way to measure the total reward from this state over time is calculating expected Returns for all possible senarios. The function to calculate it is called Value Function:

 

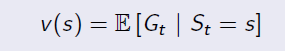
Ex. If the agent is at Class3 state, it has 0.6 and 0.4 probabilities to transite to Pass and Pub respectively. Because there are loops inside the graph, it's difficult to directly derive expected return from value function. (Forget the red labeled value, they are result...)

 

 

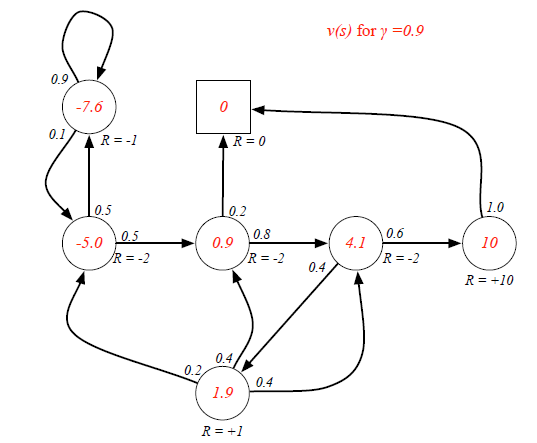
Bellman Equation helps to solve this complexity:

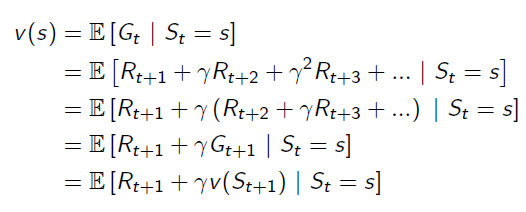
It breaks the value function into two parts: Immediate Reward and Future Reward: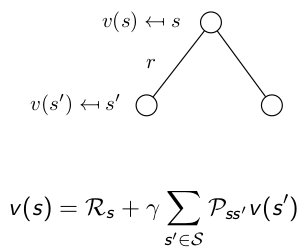The future reward is discounted by γ, and it has probabilities on different states, so actually the future reward is an expectation.

 

Now we can use Bellman Equation to solve value function: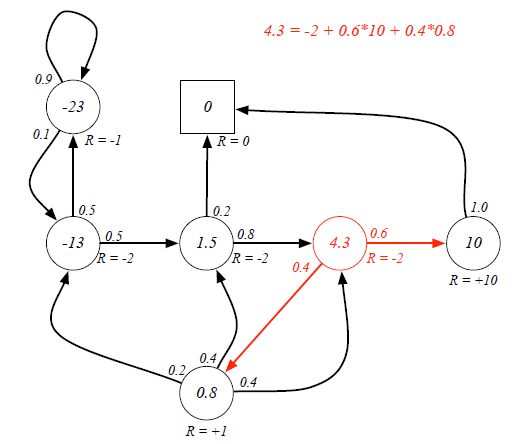

 

Markov Decision Process: MRP with Actions

Keywords: Action

Markov Decision Process adds more complexity onto MRP, it is defined by a tuple(S,A,P,R,γ), in which:

S is state space, and γ is discount factor, they are same as MRP.

A is a finite set of Actions, which is new. Then because of the existense of Action, Transition Matrix and Reward Function are all conditional on both State and Action.

P is State Transition Matrix: it is conditional on state and action at time t, which means different actions would result in different distribution of state at time t+1.

R is Reward Function conditional upon state and action: also, different actions lead to different reward, despite of the same state s.

 

A graph(from Wikipedia) helps understanding the role of actions:

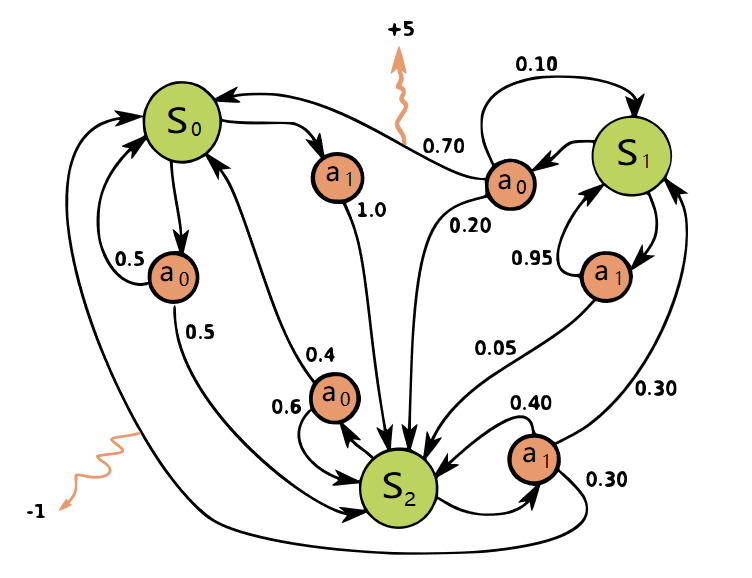
So by now, we have already had the model of the environment: all states, all possible actions and transition matrix conditional on state and actions.